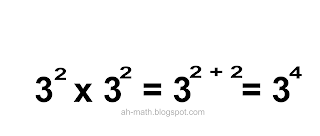Pengertian dan Macam-Macam Persamaan Kuadrat

Pengertian dan Macam-Macam Persamaan Kuadrat

August 08, 2023

0 komentar

Persamaan Kuadrat

Halo teman-teman. Apakah kamu sedang bahagia?

yuk kita mulai belajar matematika. hari ini kita akan belajar Persamaan Kuadrat.

Sebeluk kesana, kita terlebih dahulu harus mengerti apa itu kuadrat. Dalam matematika, kuadrat adalah apabila bilangan r dikalikan dengan bilangan itu sendiri sama dengan x, atau di tulis r² = x (bahasa gampangnya, kuadrat adalah angka 2 uang ditulis dengan menjorok keatas)

Berikutnya adalah persamaan kuadrat. Apa itu persamaan kuadrat?

Persamaan kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Bentuk umumnya adalah f(x) = ax² + bx + c : dengan a, b merupakan koefisien (angka yang terletak sebelum variabel) dan c adalah konstanta (angka yang berdiri sendiri), serta a ≠ 0. Penyelesaian atau pemecahan dari masalah ini disebut sebagai akar-akar persamaan kuadrat.

Macam-Macam akar persamaan kuadrat

Untuk menentukan akar-akar persamaan kuadrat kita juga bisa menggunakan rumus D = b²-4ac. Jika sudah terbentuk nilai D kita akan mudah menentukan akar-akar sebuah persamaan kuadrat. Berikut adalah jenis-jenis persamaan kuadrat secara umum :

          1.      Akar real (D ≥ 0)

Jika sebuah persamaan kuadrat diketahui nilai D > 0, maka nilai akarnya real dan berbeda.

Contoh : x² + 5x + 6 =0 ( nilai a = 1, b = 5, dan c = 6)

D = b²-4ac

    = 5²-4(1)(6)

    = 25-24

    = 1 (1>0, maka akar-akarnya akan diketahui bernilai real dan berbeda)

Bukti !

x² + 5x + 6 = 0

(x + 2)(x + 3) = 0

x + 2 = 0 atau x + 3 = 0

      x = -2               x = -3

Jika sebuah persamaan kuadrat diketahui nilai D = 0, maka nilainya real dan sama.

Contoh : x² + 4x + 4 =0 ( nilai a = 1, b = 4, dan c = 4)

D = b²-4ac

    = 4²-4(1)(4)

    = 16-16

    = 0 (0 = 0, maka akar-akarnya akan diketahui bernilai real dan sama)

Bukti !

x² + 4x + 4 = 0

(x + 2)(x + 2) = 0

x + 2 = 0 atau x + 2 = 0

      x = -2               x = -2

          2.      Akar Imajiner / Tidak Real (D < 0)

Jika sebuah persamaan kuadrat diketahui nilai D < 0, maka nilai akarnya tidak real.

Contoh : 2x² + 2x + 4 =0 ( nilai a = 2, b = 2, dan c = 4)

D = b²-4ac

    = 2²-4(2)(4)

    = 4-32

    = -28 (-28 < 0, maka akar-akarnya akan diketahui bernilai tidak real)

          3.      Akar Rasional (D = k²)

Jika sebuah persamaan kuadrat diketahui nilai D = k², maka nilai akarnya akar rasional (berupa bilangan kuadrat)

Contoh : x² + 4x + 3 =0 ( nilai a = 1, b = 4, dan c = 3)

D = b²-4ac

    = 4²-4(1)(3)

    = 16-12

    = 4 = 2² (4 >  0, maka akar-akarnya akan diketahui bernilai rasional)

Demikian sedikit ulasan materi pengertian dan macam-macam persamaan kuadrat. Kita akan sambung sub bab berikutnya pada halaman yang lain.

Terima kasih sudah balajar hari ini.

Menjadi Pintar itu mudah, menjadi manusia yang berakhlak itu yang sulit.

Jadilah manusia yang bermanfaat. Sampai jumpa pada materi berikutnya.

Operasi Pada Bilangan Berpangkat

Operasi Pada Bilangan Berpangkat

August 07, 2023

0 komentar

Operasi Pada Bilangan Berpangkat
(Perkalian-Pembagian-Pemangkatan)

Setelah kita mempelajari konsep serta notasi pada bilangan berpangkat, berikurnya kita akan membahas operasi pada bilangan berpangkat. Ada beberapa operasi pada bilangan berpangkat yang dapat kita lakukan :

1. Perkalian Pada Perpangkatan

    Perhatikan operasi perkalian pada perpangkatan berikut :

    a. 3² x 3² = (3 x 3) x (3 x 3) = 3 x 3 x 3 x 3 = 3²⁺² = 3⁴
     b. y³ x y² = (y x y x y) x (y x y) = y x y x y x y = y³⁺² = y⁵

*Bahasa gampangnya : perkalian pada perpangkatan dapat diselesaikan dengan menjumlahkan eksponen/pangkatnya (harus bilangan yang basis/ bilangan pokoknya sama)

Pada soal b. bilangan pokok/basisnya adalah sama yaitu y, maka dapat diselesaikan dengan menjumlahkan pangkatnya yaitu 3 dan 2.

2. Pembagian Pada Perpangkatan

    Pada dasarnya operasi pembagian memiliki konsep yang sama dengan operasi perkalian. Kalau operasi perkalian kita hanya menjumlah bilangan pangkatnya (dengan basis yang sama), maka untuk pembagian bilangan berpangkat kita harus mengurangi bilangan pangkatnya.
Perhatikan operasi pembagian pada perpangkatan berikut :

3. Pemangkatan Pada Perpangkatan

Pada operasi pemangkatan pada bilangan berpangkatan juga memiliki konsep yang sama. Hanya saja untuk penyelesaian kasus ini adalah dengan mengalikan bilangan pangkatnya.
Sebagai contoh :

 a. (3²)² = (3²) x (3²) = 3 x 3 x 3 x 3 = 3^2x2 = 3⁴
 a. (y²)³ = (y²) x (y²) x (y²) = y x y x y x y x y x y = y^2x3 = 3⁶
 

Notasi Pangkat

Notasi Pangkat

August 06, 2023

0 komentar

Notasi Pangkat

Setelah memahami konsep perpangkatan, selanjutnya kita akan belajar menyatakan perpangkatan dalam bentuk perkalian bilangan berulang.

Sebagai contoh :

4² = 4 x 4 = 16
4³ = 4 x 4 x 4 = 64
4⁴ = 4 x 4 x 4 x 4 = 256

4³ merupakan perpangkatan dari 4.
Bilangan 4 disebut basis atau bilangan pokok, sedangkan 3 merupakan eksponen atau pangkat.

Selesaikan soal berikut :
3³ = ... x ... x ... = ...
4³ = ... x ... x ... = ...
2⁴ = ... x ... x ... x ... = ...
5² = ... x ... = ...

Penyelesaian :

3³ = 3 x 3 x 3 = 27
4³ = 4 x 4 x 4 = 64
2⁴ = 2 x 2 x 2 x 2 =16
5² = 5 x 5 = 25

Memahami Konsep Bilangan Berpangkat

Memahami Konsep Bilangan Berpangkat

August 06, 2023

0 komentar

Memahami Konsep Bilangan Berpangkat

Sebelum mengawali pembahasan subbab bilangan berpangkat alangkah baiknya kita berdoa kepada Tuhan Yang Maha Esa semoga diberikan jalan terang dalam proses pemahaman materi yang akan saya tulis dibawah.

Sebagai pengantar mari kita pahami beberapa langkah berikut :

1. Sediakan selembar kertas serta sebuah gunting

2. Lipatlah kertas menjadi dua bagiansama besar, yaitu pada sumbu simetri lipatnya

3. Guntinglah kertas pada sumbu simetri lipatnya

4. Tumpuklah hasil guntingan kertas sehingga tepat menutupi satu dengan yang lain

5. ulangi langkah ke-2 sampai 4 sampai kertas menjadi bagian yang kecil

Dari kegiatan diatas, kita akan memperoleh hasil bahwa pengguntingan kertas ke-2 adalah 2 kali lipat dari banyak kertas hasil pengguntingan ke-1. Banyak kertas hasil pengguntingan kertas ke-3 adalah 2 kali lipat dari banyak kertas hasil pengguntingan ke-2. jika kita menggunting kertas sebanyak n kali maka banyak kertas hasil guntingan ke-n adalah

Jadi dapat disimpulkan bahwa perkalian berulang dari suatu bilangan a dapat disebut dengan perpangkatan a.

Sebagai contoh :

3 x 3 x 3 x 3 x 3 x 3 = 3⁶ (disebut perpangkatan 3 dan dibaca tiga pangkat enam)

(-4) x (-4) x (-4) = (-4)³ (disebut perpangkatan -2 dan dibaca negatif empat pangkat tiga)